- ��ɫ��Ƶ
- Vision and Values
- ��ɫ��Ƶ’s School: What to Expect
- ��ɫ��Ƶ’s Juniors: What to expect
- Collaboration with ��ɫ��Ƶ’s Girls’ School
- Diversity, Equality & Inclusion
- ��ɫ��Ƶ’s School Virtual Tour
- Term Dates
- History and Archives
- News
- Events
- Welcome from the High Master
- Welcome from the Head of ��ɫ��Ƶ’s Juniors
- High Master’s Blog
- Our Governance
- Inspections
- School Policies
- Work with Us
- Facilities & Hires
- School Uniform Shop
- Admissions
- Academic Life
- Academic – Age 7-13
- Academic – Age 13-18
- Teaching Staff
- Teaching and Learning
- Learning Support – Age 13 – 18
- Kayton Library
- Exam Results & Information
- Art
- Biology
- Chemistry
- Classics
- Computer Science
- Drama and Theatre Studies
- Economics
- Engineering
- English
- Geography
- History
- ICT
- Mathematics
- Modern Languages
- Music
- Physics
- Politics
- Theology & Philosophy
- Extended Project Qualification (EPQ)
- Careers and Universities
- Beyond the Classroom
- Wellbeing and Pastoral Care
- Our Community
Back to all news


The Mathematics Department is heavily involved in the school’s partnerships and outreach programme. This year, one of the highlights was a two-day programme of Mathematics presentations and break-out activities.
We hosted Year 10 pupils from schools in London (including Bishop Challoner School, Fulham Boys School, Grey Coat Hospital, Hammersmith Academy and West London Free School).
In addition to these sessions, our break-out activities included a bridge-building engineering challenge in which teams of six pupils constructed a load-bearing bridge exclusively out of lollipop sticks and Sellotape, spanning 50cm, which was then tested – to destruction – by incrementally adding more and more mass for the bridge to bear. The pupils also took on a cypher challenge again in teams of six, to construct a cypher using fifty 1p coins and fifteen 2p coins, and then – in half-teams – to encrypt and decrypt as much plaintext as possible. Both these challenges were greatly enjoyed by the pupils.
Elementary, my dear Watson (a report by Dr Franjic)
First, we warmed up our little grey cells by cracking a few hat puzzles. Can you conclude which colour hat you’re wearing? Easily, if you employ your powers of deduction!
Next, we stepped into the world of Boolean algebra. Boolean algebra is a branch of mathematics that deals with operations on logical values with binary variables. The concept was first introduced by George Boole in his book “The Mathematical Analysis of Logic,” and further expanded upon in his book “An Investigation of the Laws of Thought”. The primary modern use of Boolean algebra is in computer programming languages, but it also has applications in set theory and statistics. In finance, it is used in mathematical modelling of market activities. For example, in the binomial options pricing model, where there are only two possible outcomes, the Boolean variable represents an increase or decrease in the price of the security.
We introduced the basic operations: negation, conjunction and disjunction, and learned how to write out truth tables for various types of complex propositions. We had lots of fun!
Billiards and Geometry (a report by Mr Gazet)
Is it possible to hit a billiard ball on a billiards table so that the ball hits each of the sides in turn and would continue repeating the same path? In this session, we proved that as long as the ball does not start at the corner, this is possible for a rectangular i.e. normal) table if you aim parallel to the diagonal of the table. How we did this was to think about the sides of the table as mirrors, so that instead of bouncing off the side at the same angle as it hits the side, the ball carries on in a straight line. This idea of reflection is a useful one in mathematics, with lots of deeper ramifications.
We also asked what would happen with a triangular table, i.e. could we use the same ideas again? We saw that the situation was really different, and the students were left with the challenge: could they show that what we thought was true really was?
A Perfect Set of Squares (a report by Dr Hemery)
In this session, pupils were encouraged to investigate the link between a pair of positive whole numbers and a rectangle filled with squares. The process of forming and then testing a hypothesis lies right at the heart of problem-solving, and dispels the myth that mathematics is simply about rote learning one technique after another. The groups successfully unearthed the important connection between the numbers and pictures, and in so doing followed in the footsteps of Euclid – one of the most famous mathematicians of all time!

A Trip to the Cinema (a report by Dr Baxter)
We decided to send ten of our Mathmos to the cinema but wanted to do some calculations first so that our trip was well organised! If ten people were to go on the trip, how many possible combinations would there be for them to sit in a row? In fact, if Michael and Ismail were going to sit together, we wondered in how many ways this could happen, but then realised that they had fallen out, so then asked how many possibilities there would be for them to sit apart! We extended this to having Michael, Ismail and Devonte all together, then all apart and then exactly two of them together. Of course, we then had to consider the question of organising ten people into two cars in different ways! The next step is to think about how many ways we can choose five items from a wide selection of different flavours of popcorn, sweets and drinks…
Looking further ahead, we wondered if Professor Eva came back to visit ��ɫ��Ƶ’s in some years’ time with three people in her research group, Prof. Lucia with four and Prof. Phoebe with five, how many ways they could all stand in line for a photo if everyone in each research group had to stand together. Considering that it might take one minute to stand in a line, how long would it take to try out all the combinations?
A fun session with an enthusiastic group of mathmos: I even heard from some Paulines that it prompted a lively discussion at lunchtime while a group decided how to sit on a bench!
Team Challenge (a report by Ms French/Miss Cloete)
An important skill for any mathematician is the ability to work collaboratively on solving problems. During this year’s mathematics circles, students were split into teams of 4 and took part in a UKMT team challenge inspired afternoon. Teams competed in 3 rounds, with tensions running high until the final minute! The first round was a team relay; one pair from each team was required to correctly solve a question before the next pair on the team could start on their question. Teams worked on questions like “Two different digits are chosen from the four digits of 2019 and the mean is calculated. This is repeated with all possible pairs of different digits. What is the mean of their means?” and at the end of 20 minutes, the race for first place was on. The second round was everyone’s favourite, the shuttle race – here each pair in the team is given two questions; with the answer from the first question feeding into the second pair’s first question and so on. With questions like 1223-3445+56=ab, where ab is a fraction in its lowest terms, pass on the value of a” and “T is the number you will receive, Ty-2+2y=T3y-4, pass on the value of y”. There was back-and-forth between the pairs and some very tense moments while teams looked to take home the prize. The third, and final, round was the group problem solving activity. Working in a group of 4, teams tried to answer as many questions as possible in the final 10 minutes of the afternoon. How many can you get right?
Here is an example problem:

Conway’s Soldiers (a report by Mr Hewitt)
John Conway was a highly prolific British mathematician. While he made numerous contributions to the study of mathematics (such as developing the ATLAS of finite groups), he became famous for his work on recreational mathematics, earning instant celebrity status for his work on the Game of Life in particular.
Conway’s Soldiers is another mathematical game that he invented and analysed. Picture a chessboard that extends infinitely far in all directions, with a red horizontal line splitting the board in half. The first stage is the deployment stage – you are allowed to place soldiers (represented by checkers pieces) on your half of the board. You can place as many as you like anywhere below the red line. The second stage is the attack stage – using horizontal and vertical checkers moves alone (wherein one soldier jumps over another and removes them from the board), your aim is to encroach as far as possible into enemy territory above the red line. No more soldiers may be added in the attack stage.
It is relatively straightforward to reach the first, second and third rows starting with 2, 4 and 8 soldiers respectively. Somewhat surprisingly, it takes at least 20 soldiers to reach the fourth row, breaking the tantalising doubling pattern that had started to emerge. I would encourage the curious reader to attempt the problem themselves with a square grid and a handful of pieces of any kind (scraps of paper will do in a pinch). For those that want a hint, the starting arrangements required are pictured below – the soldiers marked “B” represent an alternative to those marked “A”.
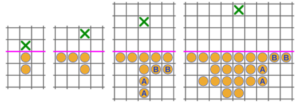
Far more surprising is the fact that, regardless of how many soldiers you start with, it is impossible to reach the fifth row in a finite number of moves. Even with millions or billions of soldiers at your disposal, you simply cannot get any further than four rows into enemy territory. Proving this remarkable result is actually not quite as challenging as it may seem, although it does require a trip into the world of invariants, monovariants and a considerable amount of summing to infinity. In the talk, we warmed up to this proof with a simpler problem involving clones escaping prison, making a brief stop at the infamous golden ratio on our way back to the final result. For a demonstration of how to reach the fifth row in an infinite number of moves, the reader can consult this webpage, replete with a rather mesmerising animation at the bottom of the page:
Constructing polygons (a report by Mr Lyster)
How many regular polygons up to 100 sides can you construct with just a ruler and a compass? The students first constructed perfect equilateral triangles and squares with no guessing and no measuring of angles. Then by bisecting angles they could get hexagons, octagons, 12-gons, 24-gons etc. Euclid described constructing a pentagon in 300BC and we used a similar method, solving a quadratic equation to construct a decagon using the golden triangle. We then discussed Gauss’s breakthrough, constructing the 17-gon, and considered fractions to get the 15-gon, 51-gon and 85-gon. Finally we matched our 3,5,17,… sequence with Fermat’s primes and his conjecture which Euler later disproved, by finding that 4294967297 is not prime, obviously without a calculator!
A Can of Worms (a report by Dr Kemp)
The session started with the challenge of estimating the thickness of a piece of sticky tape. Students used various methods to do this from folding it enough times so that the thickness could be measured to approximating the reel as a collection of circles with an average radius. Accurate results were achieved by this and the discussion moved to the exact calculation that the reel of tape is a prism with a certain volume, which was equal to the volume of the tape when unrolled as a very long, thin cuboid whose length and width is known allowing an equation for the thickness to be formed and solved giving the almost exact answer of 40 microns.
The next question related to a pasta measuring tool and estimating the number of strands of spaghetti in a serving. The geometry of the situation was discussed, noting that the optimal arrangement saw the spaghetti in a hexagonal configuration and calculating the amount of empty space. The results agreed almost exactly with practical experiment (251 strands in practice to 252 by calculation).
The students were left with the problem of estimating how many balls were required to fill a ball pit and the spherical close packing problem that ensued. This is a difficult problem going back to Kepler’s conjecture of 1611 that the two most natural arrangements of spheres (hexagonal close packing and cubic face centred) are in fact the most efficient space filling arrangements, which was proven to be true only in this century by Thomas Hales. In higher dimensions this problem has deep connections throughout Mathematics.






